
Because it's saturated, the transistor drops very little voltage between collector and emitter, resulting in an output voltage of (practically) 0 volts.
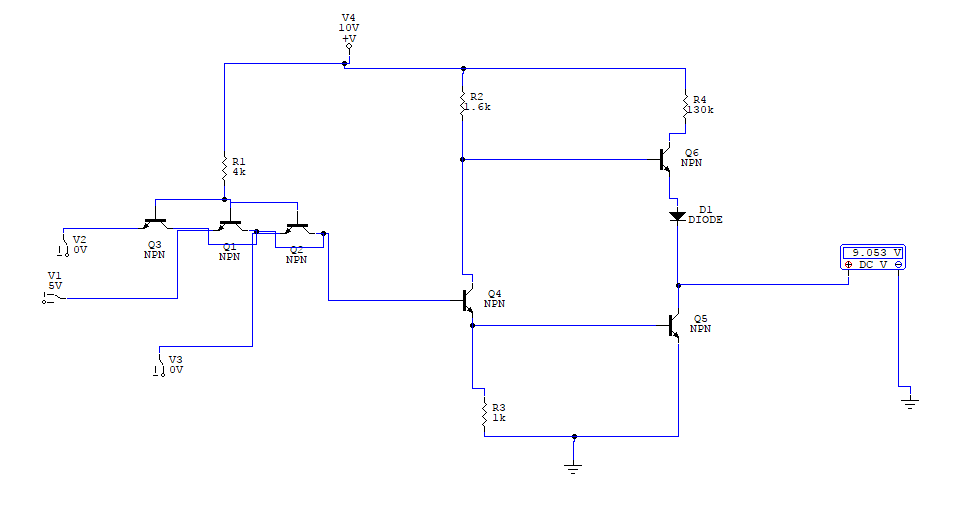
In this circuit, the transistor is in a state of saturation by virtue of the applied input voltage (5 volts) through the two-position switch. A voltage signal taken off the output of such a circuit may also serve as a representation of a single bit, a low voltage representing a binary "0" and a (relatively) high voltage representing a binary "1." Note the following transistor circuit: If a transistor circuit is designed to maximize the probability of falling into either one of these states (and not operating in the linear, or active, mode), it can serve as a physical representation of a binary bit. Transistors, when operated at their bias limits, may be in one of two different states: either cutoff (no controlled current) or saturation (maximum controlled current). This is the basic concept underlying digital computing.Įlectronic circuits are physical systems that lend themselves well to the representation of binary numbers. Consequently, any physical system capable of representing binary bits is able to represent numerical quantities, and potentially has the ability to manipulate those numbers. Because a binary bit can only have one of two different values, either 0 or 1, any physical medium capable of switching between two limiting states may be used to represent a bit. What makes binary numeration so important to the application of digital electronics is the ease in which bits may be represented in physical terms. This chapter is devoted to just that: practically applying the concept of binary bits to electric circuits.
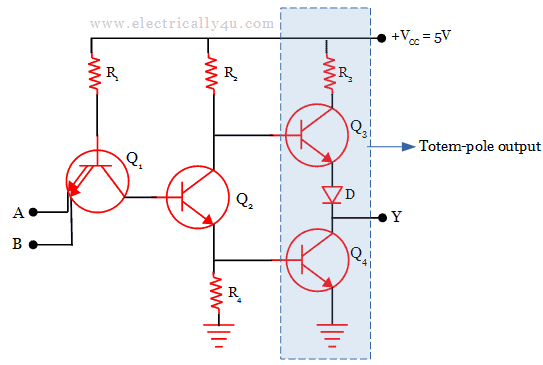
While the binary numeration system is an interesting mathematical abstraction, we haven't yet seen its practical application in electric circuits.


 0 kommentar(er)
0 kommentar(er)
